In order to move as one with
your opponent finding the true way of Taekwondo you must
control yourself according to the rhythm of motion and ride
all change. The origin of everything is the same driving
force behind all change. This has been termed both “Do”
(?[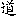 ])
and Yeok (?[
])
and Yeok (?[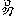 ])1).
Do is the term applied from the perspective of “non-being”
to refer to the non-distinctive nature of the absolute.2)
Yeok, on the other hand, is
the term applied from the perspective of “being”.3)
])1).
Do is the term applied from the perspective of “non-being”
to refer to the non-distinctive nature of the absolute.2)
Yeok, on the other hand, is
the term applied from the perspective of “being”.3)
What is or is not? Truly this is the distinction. From
the perspective that there is no distinction there is the
Do that never changes, penetrating all things. From the
perspective of distinction each can be different from the
other, which produces changes with Yeok that presents us
with all varieties of change in the world. With full understanding
of this you will come to know that Do and Yeok are open
to one another, and not at all different.
The rhythm immanent in change
generates Yin and Yang through Yeok and Kang and Yu through
Do. Since Yin, Yang, Kang and Yu compose Saram (Man), and
the composition proceeds as breath, there can be distinction
between Yin and Yang and between Kang and Yu in terms of
Saram. Therefore, the Samjae of Haneul (Heaven), Tang
(Earth) and Saram can be no exception, nor can anything
in Taekwondo.
To discern this sort of change in Taekwondo the best example
to look at would be that of distance. Distance is one of
the most fundamental factors in Taekwondo. It is also the
most objective one as the unity of Haneul and Tang does
not include the subjectivity of Saram. Distance in Taekwondo
is very much alive and in continuous flux. Everything that
changes, and thus everything that lives, has its own rhythm.
Therefore, when you confront your opponent, and the two
of you take up a particular distance, two rhythms are meeting
each other making one controlled at that distance. This
control is the true rhythm of TAEKWONDO. It can be within
or outside of you.
The relationship between distance and rhythm is a simple
one, and each is included in the other. Placing oneself
at a proper distance means being able to move with a proper
rhythm. Everything ideal is essentially simple. An ideal
is where difficulty and ease meet. Distance differs subtlety
from rhythm. This sort of rhythm can never be seen but rather
can be found only when you raise your vitality and harmonize
its rhythm with the world. You cannot perceive distance
in Taekwondo with your eyes; you should find it with your
mind. And you should practice Taekwondo not merely with
your mind but with your whole being.
What is the role of distance? Distance in Taekwondo concerns
attack and defense. It is a vital element in subduing one’s
opponent and protecting oneself. This attack and defense
constitutes the whole meaning behind Taekwondo’s motions,
which realize themselves in distance on the one hand while
revealing themselves in poses on the other. Here, tide
and balance when united make pose.
Why do we discuss pose? It is because pose is visible and
so simple to correct in the course of training. Flowing
rhythm becomes equipped rhythm in pose. That is, when you
make your pose its figure determines the range of rhythm
possible to you. Owing to this, your opponent’s pose
reveals the nature of his motion. To express it differently,
you can discern all his possible motions in his pose. A
good pose should not be just a stable one. Rather, a good
pose should be one that suppresses the opponent. It must
not be ‘for the sake of' subduing him, but submission
itself’.
In this respect, motion and standstill are no different
in Taekwondo, which embraces what Buddhism speaks of as
“Saek Jeuk Si Gong, Gong Jeuk Si Saek” (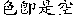 ,
,
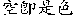 )4).
You know that everything visible is empty, which is because
you discern it not with your eyes but with your mind. In
the same manner, you can see the motion hidden in your opponent’s
pose when you look into his mind over the temptations of
his visible form. Rhythm flows along through changes and
motions. In this way, the rhythm that regulates all motions
is extended even to the calm pose of Taekwondo.
)4).
You know that everything visible is empty, which is because
you discern it not with your eyes but with your mind. In
the same manner, you can see the motion hidden in your opponent’s
pose when you look into his mind over the temptations of
his visible form. Rhythm flows along through changes and
motions. In this way, the rhythm that regulates all motions
is extended even to the calm pose of Taekwondo.